Molecular Programming

The goal of molecular programming is the systematic manipulation of matter at the molecular scale, for applications in engineering + technology and biology + medicine.
Structural DNA/RNA nanotechnology currently provides the only fabrication pipeline for truly programmable molecular structures, in the form of static and dynamic nucleic acid assemblies. But through it we can organize also other forms of matter.

Papers

Sequenceable Event Recorders (arXiv'21, Springer'23)

PID Control of Biochemical Reaction Networks (CDC'19, TAC'21)

Chemical Reaction Network Designs for Asynchronous Logic Circuits (DNA22 '16, NaCo '17)

Programming Discrete Distributions with Chemical Reaction Networks (DNA22 '16, NaCo '17)

The Formal Language and Design Principles of Autonomous DNA Walker Circuits (ACS Synthetic Biology'16)

Automated Design and Verification of Localized DNA Computation Circuits (DNA21 '15)

Programmable chemical controllers made from DNA (Nature Nanotech '13)

Two-Domain DNA Strand Displacement (MSCS'13)

Abstractions for DNA circuit design (J.R.S. Interface '12)

Design and Analysis of DNA Strand Displacement Devices using Probabilistic Model Checking (J.R.S. Interface '12)

Strand Algebras for DNA Computing (Natural Computing '11)

A Programming Language for Composable DNA Circuits (J.R.S.Interface '09)

Edited Proceedings

DNA 17

Talks

Telling Molecules What To Do (Lisbon Distinguished Lecture)

Molecular Programming (ECOOP'14)

Computing with Molecules (DCM'12)

Two-Domain DNA Strand Displacement (DCM'10)

Strand Algebras for DNA Computing (DNA '09)

Tools

DSD - DNA Strand Displacement Simulator (

J.R.S. Interface '13)

Gener - DNA Strand Displacement Reductions (

Bioinformatics '15)

Links

Correctness of DNA encodings of chemical reaction networks

DNA Computing and Molecular Programming Conferences

NYU Caltech UW Duke Oxford Aarhus Microsoft

Outreach

Inner Life of A Cell - Movie

Powering the Cell: Mitochondria - Movie

DNA Strand Displacement - Movies

Nanocrafter - Game

EteRNA - Game

Systems Biology

Reactive Systems

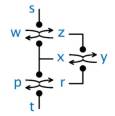
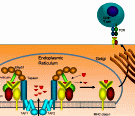
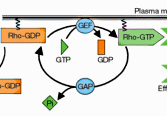
An abstract machine is a fictional information-processing device that can, in principle, have a number of different physical realizations (mechanical, electronic, biological, or software). Biochemical toolkits in cellular biology (nucleotides, amino acids, and phospholipids) can be seen as abstract machines with appropriate sets of states and operations, corresponding respectively to genes, proteins, and membranes. To understand the functioning of a cell, one must understand (at least) how the various machines interact. This involves considerable difficulties in modeling and simulations because of the drastic differences in the "programming model" of each machine, and in the time and size scales involved.

Papers

Lineage Grammars: Describing, Simulating and Analyzing Population Dynamics. (BMC Bioinformatics'14)

An Intuitive Modelling Interface for Systems Biology (DCM'09) (IJSI'13)

Abstract Machines of Systems Biology (TCSB)

Artificial Biochemistry (Algorithmic Bioprocesses)

Can a Systems Biologist Fix a Tamagotchi? (Gilles Kahn Colloquium)

Visualization in Process Algebra Models of Biological Systems (The Fourth Paradigm)

A Compositional Approach to the Stochastic Dynamics of Gene Networks (TCSB)

Compositionality, Stochasticity and Cooperativity in Dynamic Models of Gene Regulation (HFSP ournal)

Lectures

Artificial Biochemistry - Graduate Course (Trento, May 22-26 '06)

Talks

Speaking the Language of Molecules (CDE Distinguished Lacture, U.Washington)

Living Software (L'INRIA a Quarante Ans)

Artificial Biochemistry (Longo Symposium 2007)

Can a Systems Biologist Fix a Tamagotchi? (Kahn Colloquium 2007)

Abstract Machines of Systems Biology (Dagstuhl 2006)

Languages and Notations for Systems Biology (UPP'04 Invited Talk)

A Compositional Approach to the Stochastic Dynamics of Gene Networks (Concur '05)

Links

Adrian Thompson: Evolution of circuits in hardware (archive)

Membrane Computing

The basic physical operations on membranes are local fusion (two patches merging) and local fission (one patch splitting in two). When seen at the global scale of whole membranes, these local operations induce four transformations: in addition to the obvious splitting (Mito) and merging (Mate) of membranes, there are also operation, quite common in reality, that cause a membrane to eat (Endo) or spit (Exo) another subsystem. Although this is an unusual computational model, the membrane operations supports the execution of real algorithms, some of which occur in nature. Some sets of operations are Turing-complete, and can encode the other membrane operations.

Papers on
Brane Calculi

Programming Chemistry in DNA Addressable Bioreactors (Interface '14)

Brane Calculi (ENTCS, CMSB'04)

Bitonal Membrane Systems (TCS)

Where Membranes Meet Complexes (BioConcur '05)

A Universality Result for a (Mem)Brane Calculus Based on Mate/Drip Operations (IJFCS)

Papers on
BioAmbients

BioAmbients: An Abstraction for Biological Compartments (TCS)

Bioware Languages (Computing Systems - A Tribute to Roger Needham)

Lectures

Membrane Interactions

(CSSB School Rovereto, April'04)

Talks

Bitonal Membrane Systems (MeCBIC'06)

WhereMembranesMeetComplexes (BioConcur'05)

Biological Systems as Reactive Systems (ECCS'05)

Continuous Markov Processes

We introduce stochastic extensions of process algebras endowed with structural operational semantics expressed in terms of measure theory. The set of processes is organised as a measurable space by the sigma-algebra generated by structural congruence. The structural operational semantics associates to each process a set of measures over the space of processes. The measures encode the rates of the transitions from a process (state of a system) to a measurable set of processes. We prove that stochastic bisimulation is a congruence that extends structural congruence. In addition to an elegant operational semantics, our approach provides a canonic way to define metrics on processes that measure how similar two processes are in terms of behaviour.

Papers on
Logic

Continuous Markovian Logic Axiomatization and Quantified Metatheory (LMCS'12)

Modular Markovian Logic (ICALP'11)

Continuous Markovian Logic (CLS'11)

Papers on
Algebra

Stochastic Pi-Calculus Revisited (ICTAC'13)

The Measurable Space of Stochastic Processes (QEST'10, Fundamenta Informaticae)

Talks

Stochastic Pi-Calculus Revisited (ICTAC'13)

Continuous Markovian Logic (CSL'11)

Modular Markovian Logic (ICALP'11)

The Measurable Space of Stochastic Processes (QEST'10)

Natural Computability

We investigate the question of whether basic chemical kinetics (kinetics of unar yand binary chemical reactions), formulated as a process algebra, is capable of general computation. In particular, we investigate nondeterministic and probabilistic termination problems. The answers to those problems reveal a surprisingly rich picture of what is decidable and undecidable in basic chemistry.
We introduce an algebra for massive concurrent systems, called reversible structures, where terms retain bits of causal dependencies that allow one to reverse computation histories. These bits permit to trace effects of interactions, but not to the point of being able to identify the precise molecule that caused an effect. The algebra and the causal hints match a particular form of DNA computation.

Papers on
Termination

Turing Universality of the Biochemical Ground Form (MSCS)

On the Computational Power of Biochemistry (AB'08)

Termination Problems in Chemical Kinetics (CONCUR'08)

Papers on
Reversibility

Reversibility in Massive Concurrent Systems (SACS)

Reversible Structures (CMSB '11)

Talks

Termination Problems in Chemical Kinetics (CONCUR'08)

On The Computational Power of Biochemistry (AB'08)

Reversible Structures (CMSB'11)

Molecular Semantics

The semantics of programming languages is based on states and state transitions, through which one can study for example termination, nodeterminism, and concurrency. Adding rates to transitions induces quantitative meanings that can be related to stochastic and continuous dynamical systems, and to their realizations as molecular systems.

Papers on design

A Language for Modeling And Optimizing Experimental Biological Protocols (MDPI Computation'21)

From Electric Circuits to Chemical Networks (Natural Computing'19)

Experimental Biological Protocols with Formal Semantics (CMSB'18)

Molecular Filters for Noise Reduction (Biophysical Journal'18)

Syntax-Guided Optimal Synthesis for Chemical Reaction Networks (CAV'17)

Papers on verification
and approximation

Central Limit Model Checking (TOCL'19)

Reachability Computation for Switching Diffusions (HSCC'17)

A Stochastic Hybrid Approximation for Chemical Kinetics Based on the Linear Noise Approximation (CMSB'15, BioSystems'16)

Approximation of Probabilistic Reachability for Chemical Reaction Networks... (QEST'16)

Stochastic Analysis of Chemical Reaction Networks Using Linear Noise Approximation (CMSB'15)

Papers on morphisms
and bisimulation

Lumpability for Uncertain Continuous-Time Markov Chains.pdf (QEST'21)

Exact Maximal Reduction of Stochastic Reaction Networks by Species Lumping (BioInformatics'21)

Maximal aggregation of polynomial dynamical systems (PNAS'17)

Guaranteed Error Bounds on Approximate Model Abstractions through Reachability Analysis (QEST'18)

Syntactic Markovian Bisimulation for Chemical Reaction Networks (Springer'17)

Comparing Chemical Reaction Networks: A Categorical and Algorithmic Perspective (LICS'16, TCS'17)

ERODE: A Tool for the Evaluation and Reduction of Ordinary Differential Equations (TACAS'17)

Efficient Syntax-Driven Lumping of Differential Equations (TACAS'16)

Symbolic Computation of Differential Equivalences (POPL'16)

Forward and Backward Bisimulations for Chemical Reaction Networks (CONCUR'15)

Morphisms of Reaction Networks that Couple Structure to Function (BMC Systems Biology'14)

Papers on chemistry
via process algebra

On Process Rate Semantics (TCS'08)

A Process Algebra Master Equation (QEST'07)

From Processes to ODEs by Chemistry (IFIP TCS'08)

A Correct Abstract Machine for the Stochastic Pi-calculus (BioConcur'04)

Efficient, Correct Simulation of Biological Processes in Stochastic Pi-calculus (CMSB'07)

A Graphical Representation for Biological Processes in Stochastic Pi-calculus (TCSB)

Processes in Space (CiE'10, TCS 2012)

Lectures

On Process Rate Semantics

(Warsaw Lectures Extract, March'09)

Molecules as Automata - Open Lectures

(Warsaw, March&May'09)

Molecules as Automata - Summer School on Natural Computation

(BNC'08)

Process Rate Semantics - Computational and Systems Biology Course (Trento 2008)

Talks

Morphisms of Reaction Networks (CMSB'16)

Molecules as Automata (DNA'08, ECS'09)

From Processes to ODEs by Chemistry (TCS'08)

On Process Rate Semantics (MFPS'08)

A Graphical Representation for Stochastic ?-Calculus (BioConcur '05)

A Correct Abstract Machine for the Stochastic pi-calculus (BioConcur '04)

Processes in Space (CiE'10)

Pi in the Sky: Spatial Process Algebra for Developmental Biology (MeCBIC'09)

Posters

Stochastic Analysis of Chemical Reaction Networks Using Linear Noise Approximation (DNA21'15)

Tools

ERODE - SMT-based Automatic Exact Reduction of Ordinary Differential Equations (POPL '16 Artifact Evaluated)

CRNReducer - Automatic exact reduction of Chemical Reaction Networks (CONCUR '15)

Biological Models

Transport

Papers

Coupled Membrane Transporters Reduce Noise (Physical Review E.'20)

Cell Cycle Switch

At the core of the biochemical networks that regulates the cell cycle there is a switch that triggers an irreversible transition from one critical stage of cell division to the next. Its dynamical system behavior is fairly well understood, and could be achieved by many different networks. But in nature, from yeast to us, we find a specific universal structure of the network: what is special about this structure, beyond its required function? To answer this question we shift our perspective from dynamical systems to computing systems. We ask: what does the cell cycle switch compute, and how does it compute it?

Papers

Evolution of opposing regulatory interactions underlies the emergence of eukaryotic cell cycle checkpoints (SciRep'21)

Single molecules can operate as primitive biological sensors switches and oscillators (BMC SysBio'18)

Computing with biological switches and clocks (Natural Computing'18)

Efficient Switches in Biology and Computer Science (PLOS CompBio'17)

Noise Reduction in Complex Biological Switches (Scientific Reports'16)

The Cell Cycle Switch Computes Approximate Majority (Scientific Reports'12)

Transcriptional Regulation is a Major Controller of Cell Cycle Transition Dynamics (PLoS ONE)

Talks

The Cell Cycle Switch Computes Approximate Majority Robert Stewart Distinguished Lecture (Iowa State 2014)

Posters

Evolution of Simple Systems to Complex Behaviours (King's College PhD Symposium'16)

Analyzing Efficiency of Biological Switches (SSBSS'15)

Evolution of Biological Switches (King's College PhD Symposium'15)

Phosphorelays

Organisms employ a variety of signalling systems to sense and react to their environment. Among the most basic, commonly found in bacteria, lower eukaryotes and plants, are the so-called phosphorelays. These systems transfer sensor information (typically from the cellular membrane) very economically through a chain of chemical reactions.
Despite their widespread use and simple architecture, we are still far from a full understanding of the signal-processing capabilities of phosphorelays.

Papers

Unlimited multistability and Boolean logic in microbial signaling (J.R.S. Interface)

Phosphorelays provide tunable signal processing capabilities for the cell (PLOS CompBio)

Response Dynamics of Phosphorelays Suggest Their Potential Utility in Cell Signaling (J.R.S. Interface)

Immune System

Major Histocompatibility Complex (MHC) class I molecules are a key component of the innate immune system. They continuously select a signature of the cell contents (fragments of any protein present) and present it to the cell surface, where it can be inspected by cytotoxic T lymphocytes that destroy virus-infected and cancerous cells based on such signature. In this mechanism there is a trade-off between speed and accuracy of presentation: we study how various molecular components contribute to optimizing this process.

Papers

A Peptide Filtering Relation Quantifies MHC Class I Peptide Optimization (PLoS Computational Biology)

Projects

A Stochastic ?-Calculus Models of MHC Class I Antigen Presentation (Computational Biology MPhil Project)

Links

Selector function of MHC I molecules is determined by protein plasticity

Computational Modeling of Immune System Processes

Pi-Calculus Models

We use stochastic pi-calculus to represent and then simulate interactions within protein networks. The pi-calculus approach allows a biological system to be programmed in a scalable manner, by allowing models of individual proteins to be directly composed to form subsystems, which can in turn be composed together to form larger systems. This allows new components to be added incrementally without having to re-wire the existing model, which also improves the usability of models. Furthermore, the modular structure of the biological system and the pi-calculus model are in direct correspondence.

Papers

Computational Modeling of the EGFR Network Elucidates Control Mechanisms Regulating Signal Dynamics (BMC Systems Biology)

A Process Model of Rho GTP-binding Proteins (FBTC'07) (TCS)

A Process Model of Actin Polymerisation (FBTC'08) (ENTCS)

Lectures

Biochemical Systems as Reactive Systems - Bioinformatics Master Course (Cabridge '16)

Talks

Biological Networks in Stochastic Pi-Calculus (Imperial College London 2005)